Uma recente pesquisa mediu a capacidade de adultos para identificar conteúdos falsos e enganosos em plataformas online, como redes sociais. Os resultados indicaram que, entre os países pesquisados, pessoas adultas identificam um conteúdo falso 60% das vezes, em média. O Brasil foi um dos países que mais se afastou dessa média, como mostra o gráfico.




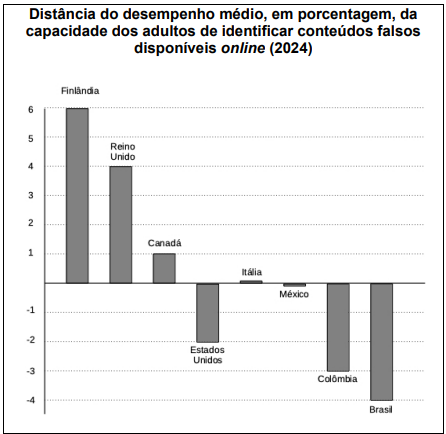
ORGANIZAÇÃO PARA A COOPERAÇÃO E DESENVOLVIMENTO ECONÔMICO (OECD). The OECD Truth Quest Survey: Methodology and Findings. (OECD Digital Economy Papers, No.369). Paris: OECD Publishing, 2024. [Adaptado].

Com base nessas informações, considerando que o gráfico apresenta todos os países pesquisados, o desvio padrão da capacidade média dos adultos de identificar conteúdos falsos, entre esses países, é, aproximadamente,

Leia o texto a seguir.

O monge e matemático italiano Luigi Guido Grandi (1671-1742) foi pioneiro no estudo de uma série infinita que gerou intensos debates filosóficos, composta pela soma infinita dos números 1 e -1:

1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + ⋯

Para Grandi, essa série mostrava que a criação a partir do nada era perfeitamente plausível. Assim como este pensamento, um outro aspecto gerador de debates foi o uso de parênteses, pois as diferentes disposições de parênteses na série levavam a interpretações e a resultados distintos.

MURTAGH, J. The Paradox of 1 – 1 + 1 – 1 + 1 – 1 + … Why a mathematician thought this infinite series explained how God created the universe. Scientific American,2024. [Adaptado]

Com base no texto, considere uma soma similar, porém, finita, contendo exatamente mil números (contando a quantidade de “1” e de “-1”, dentro ou fora dos parênteses), com parênteses dispostos conforme o seguinte padrão:

1 − (1 + 1) − (1 + 1 − 1) + 1 − (1 + 1) − (1 + 1 − 1) + 1 − ⋯

O resultado dessa expressão é

Um investidor aplicou seu capital em um fundo de renda fixa que oferecia uma taxa de 8% ao ano, a juros compostos. Após seis anos, ele transferiu o montante acumulado para um novo fundo, que oferecia um rendimento de 6% ao ano, também com capitalização composta, e manteve o valor aplicado por mais um ano. Considerando C o capital inicial investido no primeiro fundo, a diferença entre o valor dos juros recebido no primeiro fundo e o valor dos juros recebido no segundo é dada pela expressão

Leia o texto a seguir.
O desenvolvimento do pensamento algébrico é essencial para utilizar modelos matemáticos na compreensão, representação e análise de relações quantitativas de grandezas e, também, de situações e estruturas matemáticas, fazendo uso de letras e outros símbolos. Para esse desenvolvimento, é necessário que os alunos identifiquem regularidades e padrões de sequências numéricas e não numéricas, estabeleçam leis matemáticas que expressem a relação de interdependência entre grandezas em diferentes contextos, bem como criar, interpretar e transitar entre as diversas representações gráficas e simbólicas, para resolver problemas por meio de equações e inequações, com compreensão dos procedimentos utilizados.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2017. [Adaptado].

De acordo com a Base Nacional Curricular Comum, a trajetória dos objetos de conhecimento relacionados à álgebra, durante os anos do Ensino Fundamental, indica que o pensamento algébrico começa a ser desenvolvido no

Leia o texto a seguir.
Com base nos recentes documentos curriculares brasileiros, a BNCC leva em conta que os diferentes campos que compõem a Matemática reúnem um conjunto de ideias fundamentais que produzem articulações entre eles: equivalência, ordem, proporcionalidade, interdependência, representação, variação e aproximação. Essas ideias fundamentais são importantes para o desenvolvimento do pensamento matemático dos alunos e devem se converter, na escola, em objetos de conhecimento. [...]
Nessa direção, a Base Nacional Curricular Comum (BNCC) propõe cinco unidades temáticas, correlacionadas, que orientam a formulação de habilidades a serem desenvolvidas ao longo do Ensino Fundamental, na área de Matemática. Cada uma delas pode receber ênfase diferente, a depender do ano de escolarização.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2017. [Adaptado].

As unidades temáticas a que se refere o documento são: