120 Questões de concurso encontradas
Página 3 de 24
Questões por página:
Considere um processo de Poisson em que Nt representa a quantidade de ocorrências registradas até o instante t, de modo que P(Nt = n) = (n!)-1 × e-λt (λt)n . Considere, ainda, que a probabilidade de transição do estado i para o estado j seja dada por pij(t) = [ ( j - i ) ! ]-1 × e-λt ( λ t )j - i . Nesse caso, se p1,2 = p1,3(s) e se s → t, então λ > 2
Considere que, na fila do tipo M/M/1/K, o sistema seja finito e comporte até K elementos. Nesse caso, é correto afirmar que a probabilidade limite de haver Nt elementos no sistema no instante t é dada por pn (t) = P(Nt = n) →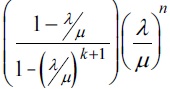 
em que λ é a taxa de chegadas por unidade de tempo de elementos na fila e μ é a taxa de atendimentos por unidade de tempo, e que tal probabilidade para a fila M/M/1 é obtida no limite K → ∞.
Para um processo AR(1), é correto afirmar que essa função é expressa na forma f(λ) = σ x { 2π ( 1-2Φcosλ ) } -1, em que |λ| ≤ π e |Φ| > 1.
