2. Questões de Concurso

Filtrar

Questões por página:

Segundo a Associação Brasileira de Proteína Animal (ABPA), os maiores produtores de carne de frango em 2022 estão apresentados no gráfico a seguir.



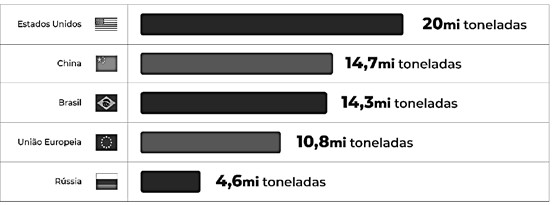
Imagem associada para resolução da questão



Disponível em: <https://nutrimosaic.com.br/como-produzir-carne-de-frango-dequalidade/>. Acesso em: 11 jan.2025.



Com base nas informações do gráfico, a produção brasileira de carne de frango corresponde, aproximadamente, a que percentual da produção total desses cinco países em 2022?

A seguir, estão listados os salários, em milhares de reais, de 10 funcionários de uma empresa: 10,11,12,12,14,14,15,16,18, 18. A média e a mediana desses valores são, respectivamente,
Um lote de 5 unidades de um produto está sendo inspecionado, e cada unidade pode ser aprovada ou reprovada, de forma independente, com probabilidades iguais para ambos os resultados. Qual é a probabilidade de exatamente 3 unidades serem aprovadas?
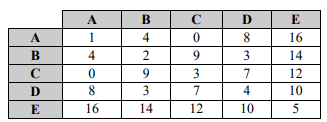
Imagem associada para resolução da questão

A tabela precedente ilustra um exemplo de matriz de variância e covariância com cinco variáveis A, B, C, D e E.

Com base nessa matriz, a variável que apresenta a maior dispersão de dados e o par de variáveis que apresenta a relação linear mais forte são, respectivamente,
Considere que um determinado estudo tenha apresentado a equação de regressão linear simples reproduzida a seguir, em que Y é a variável dependente e X é a variável independente.

Y = 4 ˗ 0,2 × X

Com base na equação e nas informações apresentadas na situação hipotética precedente, pode-se afirmar que, para cada unidade de aumento em X, espera-se
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo