Questões de Concurso

Sobre o Teste de Kruskal-Wallis, analise as afirmativas a seguir.

I. Em sua fórmula são utilizados os postos das amostras estudadas.

II. Não exige que as amostras individuais sigam a distribuição normal, mas todas as amostras combinadas devem seguir a distribuição normal.

III. É utilizado para comparar a variância de várias populações.

IV. É um teste unilateral à direita.

V. Sua estatística de teste H pode ser aproximada por uma distribuição Qui-quadrado com k-1 graus de liberdade, sendo k a quantidade de amostras.

Estão corretas apenas as afirmativas

O tempo gasto por uma impressora para imprimir uma página é uma variável aleatória que segue uma distribuição Normal com média de 10 segundos e desvio-padrão de 3 segundos. Após um problema técnico, foi coletada uma amostra aleatória de 36 impressões para averiguar se houve um aumento no tempo gasto para realizar a impressão. Considere que a variância se manteve a mesma e, ainda, 2% de significância. Calcule o poder do teste se a verdadeira média de tempo é 12 segundos.

(Informações adicionais: Z_0.01 = –2.32   Z_0.02 = –2.05   Z_0.03 = –1.88   Z_0.04 = –1.75   Z_0.05 = –1.64.)

Seja f(x, y) uma função de densidade de probabilidade conjunta das variáveis aleatórias X e Y, sua função de densidade de probabilidade é:

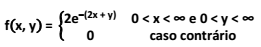
Qual a probabilidade de P(X < Y)?