Questões de Concurso
Filtrar
3.537 Questões de concurso encontradas
Página 202 de 708
Questões por página:
Questões por página:
A vibração, em mm/s, nos sensores instalados em determinada máquina é uma variável aleatória contínua X cuja função de densidade de probabilidade é dada por f(x) = 4xe-2x, em que x > 0.
Com base nessas informações, julgue o item que se segue.
A probabilidade de ocorrer o evento [X = 3 mm/s] é nula.
A vibração, em mm/s, nos sensores instalados em determinada máquina é uma variável aleatória contínua X cuja função de densidade de probabilidade é dada por f(x) = 4xe-2x, em que x > 0.
Com base nessas informações, julgue o item que se segue.
O valor esperado da variável aleatória X é igual ou superior a 2 mm/s.
A vibração, em mm/s, nos sensores instalados em determinada máquina é uma variável aleatória contínua X cuja função de densidade de probabilidade é dada por f(x) = 4xe-2x, em que x > 0.
Com base nessas informações, julgue o item que se segue.
A variável aleatória Y = √X tem distribuição normal (ou gaussiana).
A vibração, em mm/s, nos sensores instalados em determinada máquina é uma variável aleatória contínua X cuja função de densidade de probabilidade é dada por f(x) = 4xe-2x, em que x > 0.
Com base nessas informações, julgue o item que se segue.
A variável aleatória X possui desvio padrão inferior a 1 mm/s.
Concurso:
TCE-PR
Disciplina:
Estatística
Os métodos A e B utilizados na construção de casas populares proporcionam custos médios (por metro quadrado) respectivamente iguais a μA e μB, e variâncias populacionais 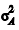 e
e 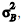 , respectivamente. Os custos seguem distribuições normais tais que
, respectivamente. Os custos seguem distribuições normais tais que 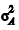 ≠
≠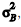 . Em um estudo estatístico realizado para comparar esses custos médios mediante aplicação de um teste t de Student para comparação de duas médias, as hipóteses foram H0: μA = μB e H1: μA ≠ μB. O quadro a seguir apresenta informações a respeito desse estudo estatístico.
. Em um estudo estatístico realizado para comparar esses custos médios mediante aplicação de um teste t de Student para comparação de duas médias, as hipóteses foram H0: μA = μB e H1: μA ≠ μB. O quadro a seguir apresenta informações a respeito desse estudo estatístico.
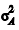 e
e 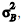 , respectivamente. Os custos seguem distribuições normais tais que
, respectivamente. Os custos seguem distribuições normais tais que 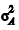 ≠
≠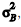 . Em um estudo estatístico realizado para comparar esses custos médios mediante aplicação de um teste t de Student para comparação de duas médias, as hipóteses foram H0: μA = μB e H1: μA ≠ μB. O quadro a seguir apresenta informações a respeito desse estudo estatístico.
. Em um estudo estatístico realizado para comparar esses custos médios mediante aplicação de um teste t de Student para comparação de duas médias, as hipóteses foram H0: μA = μB e H1: μA ≠ μB. O quadro a seguir apresenta informações a respeito desse estudo estatístico.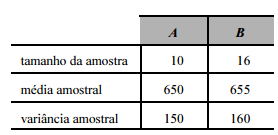
Considerando-se as informações no quadro e que as amostras sejam independentes, é correto afirmar que o valor absoluto da estatística desse teste (|T|) é