Questões de Concurso
Filtrar
3.619 Questões de concurso encontradas
Página 385 de 724
Questões por página:
Com relação ao modelo de regressão linear simples e ao conceito de correlação, julgue os itens a seguir.
Se, em um modelo de regressão linear simples, a relação entre a variável resposta (Y ) e a variável explicativa ( X ) é uma reta com 30° de inclinação positiva, então a forma do modelo é 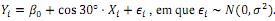
Em um modelo de regressão linear múltipla, o coeficiente de determinação é igual ao coeficiente de determinação ajustado apenas se o tamanho amostral for suficientemente grande.
Julgue os próximos itens, referentes à inferência estatística.
O método de estimação de parâmetros que consiste em determinar a função esperança (E (X) e igualar a média amostral (X) para se obter um estimador para a média de uma variável aleatória é denominado de método aritmético.
Julgue os próximos itens, referentes à inferência estatística.
No teste de hipóteses H0:µ = µ0 contra H1:µ ≠ µ0, em que os dados são provenientes de uma distribuição normal com variância conhecida, se a probabilidade de ocorrência do erro tipo I (α) for 5%, a probabilidade de ocorrer o erro tipo II (β) é igual a 20%.
Se o preço do petróleo, a cada mês, aumenta US$ 1 com probabilidade p ou diminui US$ 1 com probabilidade 1– p então a probabilidade de o preço do petróleo não sofrer alterações em um período de 12 meses é determinada a partir de uma distribuição hipergeométrica.