Questões de Concurso
Filtrar
3.537 Questões de concurso encontradas
Página 590 de 708
Questões por página:
Questões por página:
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
O tempo total para a análise de um processo trabalhista, que chega a um Tribunal Regional do Trabalho, é dado pela soma dos tempos dos 3 analistas, que o examinam. Sejam Xi, i = 1,2,3, as variáveis aleatórias que representam os tempos, em dias, para análise dos analistas 1,2 e 3, respectivamente. Sabe-se que o vetor 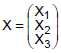 tem distribuição normal multivariada com vetor de médias dado por
tem distribuição normal multivariada com vetor de médias dado por 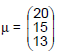 e matriz de covariâncias dada por
e matriz de covariâncias dada por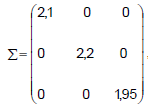 , onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
, onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
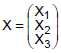 tem distribuição normal multivariada com vetor de médias dado por
tem distribuição normal multivariada com vetor de médias dado por 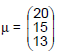 e matriz de covariâncias dada por
e matriz de covariâncias dada por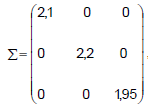 , onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2.
, onde os valores do vetor μ, são dados em dias e os da matriz Σ em (dias)2. Um processo é selecionado aleatoriamente dentre todos os processos que chegam àquele órgão. A probabilidade do tempo total para análise se situar entre 42 dias e 45 dias, em %, é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de 16 trabalhadores será selecionada e sejam X1, X2, ...X16 as idades observadas e 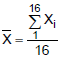 a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
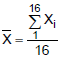 a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
a média desta amostra. Sabendo-se que a probabilidade de X ser superior a 30 anos é igual a 0,919, o valor de μ, em anos, é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de n trabalhadores será selecionada e sejam X1, X2, ... Xn as idades observadas e 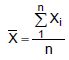 a média desta amostra. Desejando-se que o valor absoluto da diferença entre
a média desta amostra. Desejando-se que o valor absoluto da diferença entre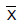 e sua média seja menor do que 6 meses, com probabilidade de 95,4%, o valor de n deverá ser igual a
e sua média seja menor do que 6 meses, com probabilidade de 95,4%, o valor de n deverá ser igual a
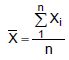 a média desta amostra. Desejando-se que o valor absoluto da diferença entre
a média desta amostra. Desejando-se que o valor absoluto da diferença entre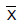 e sua média seja menor do que 6 meses, com probabilidade de 95,4%, o valor de n deverá ser igual a
e sua média seja menor do que 6 meses, com probabilidade de 95,4%, o valor de n deverá ser igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
mostrar texto associado
Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
O valor de K, em anos, tal que P( X − μ < k) = 0,758 é igual a
Concurso:
TRT - 3ª Região (MG)
Disciplina:
Estatística
Tendo por base:
I. o teorema: “Se X for uma variável aleatória contínua com função de distribuição acumulada F, então a variável aleatória U = F(x) tem distribuição uniforme contínua no intervalo [0,1].
II. os números aleatórios u1 = 0,16; u2 = 0,35 e u3 = 0,52, gerados de uma distribuição uniforme contínua no intervalo [0,1].
III. que o logaritmo natural dos números 0,84; 0,65 e 0,48 são dados, respectivamente, por − 0,17; − 0,43 e − 0,73.
Os valores simulados de uma distribuição exponencial com variância 9 a partir de u1, u2 e u3, são dados respectivamente por