Questões de Concurso
Filtrar
3.621 Questões de concurso encontradas
Página 286 de 725
Questões por página:
Questões por página:
Concurso:
TCE-PR
Disciplina:
Estatística
O tempo de vida, X, em horas, de lâmpadas de certa fabricação tem distribuição exponencial com média de 8000 horas. O tempo de vida mediano dessas lâmpadas é, em horas, igual a
Dados:
ln (0,4) = - 0,916 e
ln(0,5) = - 0,693
Concurso:
TCE-PR
Disciplina:
Estatística
Em uma fábrica existem 3 máquinas A, B e C que produzem diariamente 10.000 peças. Sabe-se que A, B e C produzem, respectivamente, 2000, 5000 e 3000 peças. Da produção de A, B e C, respectivamente, 5%, 10% e 20% são defeituosas. Seleciona-se uma peça ao acaso e verifica-se que é defeituosa. A probabilidade de ela ser proveniente da máquina C é
Concurso:
TCE-PR
Disciplina:
Estatística
Suponha que o número de acidentes que ocorrem em uma estrada segue uma distribuição de Poisson com média de 1 acidente a cada 200 km. A probabilidade de que em 500 km ocorra no máximo 1 acidente é
Dados:
e-1 = 0,368
e-2,5 = 0,082
Concurso:
TCE-PR
Disciplina:
Estatística
Relativamente a um modelo de regressão linear com heterocedasticidade considere as seguintes afirmações:
I. Os estimadores de mínimos quadrados usuais são viciados.
II. As estimativas das variâncias dos parâmetros permanecem não viciadas.
III. Os estimadores de mínimos quadrados usuais não terão variância mínima.
IV. A análise de resíduos é uma das formas de se detectar a existência de heterocedasticidade.
Dentre as afirmações acima, são verdadeiras APENAS
Concurso:
TCE-PR
Disciplina:
Estatística
mostrar texto associado
O tempo X que um indivíduo leva para memorizar determinado material é uma variável aleatória normal com média µ minutos e desvio padrão de 7 minutos. Um psicólogo, interessado em estimar µ, selecionou uma amostra de n indivíduos, ao acaso, e observou o valor da estatística 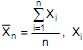 = tempo de memorização do i-ésimo indivíduo da amostra. Desejando-se que o valor observado para
= tempo de memorização do i-ésimo indivíduo da amostra. Desejando-se que o valor observado para 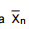 não difira de µ por mais de 1 minuto com probabilidade de 0,954, o valor de n deverá ser
não difira de µ por mais de 1 minuto com probabilidade de 0,954, o valor de n deverá ser
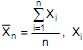 = tempo de memorização do i-ésimo indivíduo da amostra. Desejando-se que o valor observado para
= tempo de memorização do i-ésimo indivíduo da amostra. Desejando-se que o valor observado para 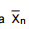 não difira de µ por mais de 1 minuto com probabilidade de 0,954, o valor de n deverá ser
não difira de µ por mais de 1 minuto com probabilidade de 0,954, o valor de n deverá ser