Questões de Concurso
Filtrar
3.537 Questões de concurso encontradas
Página 631 de 708
Questões por página:
Considere que a distribuição dos salários dos funcionários em um setor público está representada por um histograma conforme abaixo, em que no eixo vertical constam as densidades de frequências, em (R$) -1. Densidade de frequência de um intervalo de classe é o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.
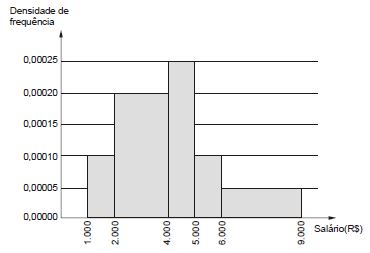
Considerando que todos os intervalos classe são fechados à esquerda e abertos à direita, a porcentagem P dos funcionários que ganham no mínimo R$ 2.000,00 e menos que R$ 6.000,00 é tal que
Em dezembro de 2011 foi realizado um levantamento em uma empresa que proporcionou a tabela de frequências relativas abaixo, referente aos salários de seus empregados, observando que 3m + n = 25%. 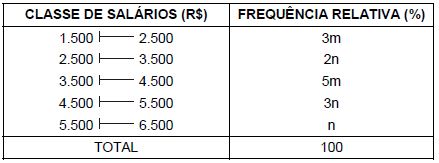
O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos num intervalo de classe são coincidentes com o ponto médio deste intervalo. O valor da mediana (Md) foi obtido pelo método da interpolação linear. Então, tem-se que