Questões de Concurso

Em uma cidade foi realizada uma pesquisa entre 600 eleitores, escolhidos aleatoriamente, com relação à preferência entre 2 candidatos X e Y para o cargo de prefeito. Esta pesquisa forneceu 2 grupos de eleitores, sendo 375 homens e 225 mulheres. Cada eleitor forneceu uma e somente uma resposta, na pesquisa, se preferia X ou Y.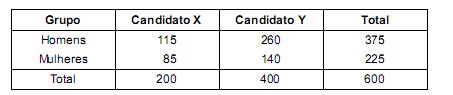



O objetivo é verificar, com relação a estes eleitores, se a preferência pelos candidatos depende do sexo, utilizando o teste qui-quadrado a um determinado nível de significância a.

Dados:

Valores críticos da distribuição qui-quadrado [P(qui-quadrado com n graus de liberdade)


É correto afirmar que

Durante 36 dias, observou-se, diariamente, a quantidade produzida de peças por duas máquinas de marcas M₁ e M₂, independentemente. Um fabricante verificou que subtraindo diariamente da quantidade de peças produzidas por M₁ a quantidade produzida por M₂ obteve a presença de sinal positivo nas diferenças de 20 produções e sinal negativo nas 16 restantes, não ocorrendo diferença nula. Aplicando o teste dos sinais para decidir se a proporção populacional de sinais positivos (p) é igual a 0,50, ao nível de significância de 5%, ele considerou as hipóteses H₀: p = 0,50 (hipótese nula) contra H₁: p ≠ 0,50 (hipótese alternativa). Com a aproximação da distribuição binomial pela normal sem a correção de continuidade, foi apurado o valor do escore r correspondente para comparação com o valor crítico da distribuição normal padrão (Z) tal que a probabilidade P(|Z| ≤ 1,96) = 95%. Então, o fabricante, ao nível de significância de 5%,

Uma indústria produz uma peça em que uma amostra aleatória de 144 peças apresentou um peso médio igual a 19,5 kg. O desvio padrão da população dos pesos destas peças, considerada de tamanho infinito e normalmente distribuída, é igual a 2 kg. Deseja-se testar a hipótese de que a média µ da população é igual a 20 kg, a um nível de significância a. Foram formuladas as hipóteses H₀: μ = 20 kg (hipótese nula) contra H₁: μ ≠ 20 kg (hipótese alternativa). Considerando que na distribuição normal padrão (Z) as probabilidades P(Z > 2,58) = 0,005 e P(Z > 1,96) = 0,025, então

Em uma distribuição uniformemente distribuída sobre o intervalo 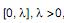extraiu-se uma amostra aleatória de 10 elementos, com reposição. O maior valor dos elementos desta amostra apresentou um valor igual a M. Com isto, obteve-se que o estimador de máxima verossimilhança da variância da população foi igual a 27. O estimador de máxima verossimilhança da média da população é

Sabe-se que E₁ = 2X₁ + mX₂ + nX₃ e E₂ = 3mX₁ + 2nX₂ + 5X₃ são 2 estimadores não viesados utilizados para a média µ diferente de zero de uma população normal com variância unitária. Considere que (X₁, X₂, X₃) é uma amostra aleatória de tamanho 3 extraída, com reposição, desta população, sendo m e n parâmetros reais. Entre os 2 estimadores, o mais eficiente apresenta uma variância igual a