Questões de Concurso

Seja (X, Y, Z) uma amostra aleatória de tamanho 3 extraída, com reposição, de uma população normal de média µ diferente de zero. Dado que o estimador E = x⁄2 + y⁄3 + KZ , sendo K um parâmetro real, para a média µ é não viesado, então o valor de K é tal que

De uma população finita, normalmente distribuída e de tamanho N, é extraída uma amostra aleatória, sem reposição, de tamanho 64. O desvio padrão populacional é igual a 2,5 e a amplitude do intervalo de confiança de 95% para a média desta população apresentou o valor de 0,98. Se na distribuição normal padrão (Z) a probabilidade P(Z > 1,96) = 0,025, então

Em uma pesquisa eleitoral realizada com 600 eleitores escolhidos aleatoriamente, 360 mostraram-se favoráveis ao candidato X. Deseja-se construir um intervalo de confiança de 95% para a proporção de eleitores favoráveis ao candidato X com base nessa amostra. Para isto, considerou-se normal a distribuição da frequência relativa dos eleitores que são favoráveis ao candidato X, a população de tamanho infinito e que na distribuição normal padrão (Z) a probabilidade P(|Z| ≤ 1,96) = 95%. A amplitude deste intervalo é igual a

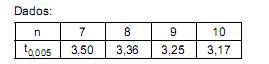
As medidas dos comprimentos de uma peça fabricada por uma empresa apresentam uma distribuição normal com desvio padrão desconhecido. Uma amostra aleatória de 9 peças apresentou uma média igual a 85 cm e um desvio padrão igual a 15 cm. Considerando a população de tamanho infinito e t_0,005 o quantil da distribuição t de Student para teste unicaudal tal que P(t > t_0,005) = 0,005 com n graus de liberdade, obteve-se, com base nessa amostra, um intervalo de confiança de 99% para a média populacional. Este intervalo de confiança, em cm, é igual a

O intervalo de confiança [224,8; 233,0] para a média populacional de uma variável X, normalmente distribuída, foi obtido por meio de uma amostra aleatória de tamanho 100. Para a obtenção do intervalo considerou-se a população de tamanho infinito, um nível de confiança de 90% e a informação de que na distribuição normal padrão (Z) a probabilidade P(Z > 1,64) = 0,05. A variância populacional da variável X é, no caso,