Questões de Concurso

Considere as seguintes afirmações:

I. Na análise de componentes principais a informação contida em um vetor aleatório p-dimensional é substituída pela informação contida num vetor aleatório q-dimensional (q < p), de variáveis aleatórias correlacionadas, denominadas pelo nome de componentes principais.

II. O escalonamento multidimensional é uma técnica matemática apropriada para representar n elementos num espaço de dimensão menor que o original, levando-se em consideração a similaridade que os elementos têm entre si.

III. Na análise de agrupamentos nenhuma variável é definida como dependente ou independente.

Dentre as afirmações acima são verdadeiras APENAS

A função de probabilidade conjunta das variáveis X e Y é dada por: f (x,y) = 1⁄32 (x² + y² ), x = 0,1,2,3 e y = 0,1 Nessas condições, a média de Y e P(X + Y = 3) são dados, respectivamente, por

Considere as seguintes afirmações:

I. Uma intervenção que afeta uma série temporal pode mudar o nível da série, podendo também afetar a sua variabilidade.

II. De um modo geral, a análise espectral de séries temporais estacionárias decompõe a série em componentes senoidais com coeficientes aleatórios não correlacionados.

III. Para o modelo Z_t = 3 + a_t − 0,5a_{t − 1}, onde a_t é ruído branco de média zero e variância σ², a previsão de origem t e horizonte 2 é igual a 3 − 0,5a_t.

IV. Se a_t é ruído branco de média zero e variância σ² um modelo do tipo Z_t = φZ_{t − 12} + a_t, |φ| < 1, é estacionário de médias móveis sazonal.

Dentre as afirmações acima são verdadeiras APENAS

Seja 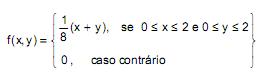a função densidade de probabilidade da variável aleatória bidimensional contínua (X,Y). A esperança condicional de Y dado que X vale 1, denotada por E(Y | X = 1), é igual a