Questões de Concurso

Seja X uma variável aleatória normal bivariada com vetor de médias e matriz de covariâncias dadas, respectivamente, por: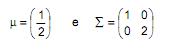



Sejam os vetores A = (2 , 0) e B = (1 , 1). Nessas condições, é verdade que a distribuição de

Uma urna contém 2 bolas verdes, 5 amarelas e 3 pretas. Selecionam-se 5 bolas aleatoriamente e sem reposição da urna. Sejam:

X = número de bolas amarelas selecionadas,

Y = número de bolas pretas selecionadas, f(x, y) a função de probabilidade da variável aleatória bidimensional (X,Y).

Nessas condições f(3,1) é igual a

Seja 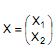um vetor de variáveis aleatórias e seja 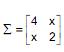sua matriz de covariâncias. Seja λ a primeira componente principal da matriz ∑ . Sabendo que a proporção da variância total de X que é explicada por λ é 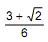o valor de x é

Uma variável aleatória U tem distribuição uniforme contínua no intervalo [α, 3α]. Sabe-se que U tem média 12. Uma amostra aleatória simples de tamanho n, com reposição, é selecionada da distribuição de U e sabe-se que a variância da média dessa amostra é 0,1. Nessas condições, o valor de n é