Questões de Concurso

Em uma repartição pública, verifica-se a existência de 5 valores de salários, referentes a um determinado cargo. A tabela abaixo fornece a quantidade de funcionários que recebe cada valor de salário.



Sabendo-se que 4X + 5Y = 60, a relação entre os valores da média aritmética (Me), da mediana (Md) e da moda (Mo) dos salários é

Considere a tabela de frequências absolutas abaixo, correspondente aos salários dos 80 funcionários lotados em um órgão público.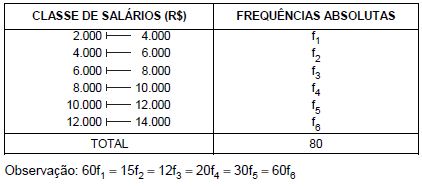

Suponha que uma instituição financeira criou um fundo de investimento onde o ativo é aplicado em uma combinação de Letras de Câmbio do Agronegócio - LCA com Letras de Câmbio Imobiliárias - LCI. Supondo-se que a variável L que representa o lucro mensal do fundo, em milhares de reais (MR), seja dada por: L = AX, sendo A o vetor de constantes dado por A = (2 1) e 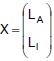 o vetor de variáveis aleatórias, onde L_A e L_I representam, respectivamente, os lucros mensais das letras LCA e LCI.

Suponha que L_A tem distribuição normal com média 80MR e desvio padrão 3MR; que L_I tem distribuição normal com média 70MR e desvio padrão de 8MR e que essas duas variáveis são independentes. Nessas condições, a probabilidade do lucro mensal de tal investimento ser um valor no intervalo (233MR ; 242MR) é igual a

Sabe-se que o vetor aleatório  tem distribuição normal bivariada com vetor de médias   e matriz de covariâncias 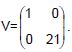 . Uma amostra aleatória [( X₁ , Y₁ , ....( X_n , Y_n )], simples, com reposição de tamanho n é selecionada da distribuição de P.

Considere a variável aleatória 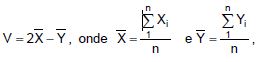 , são as respectivas médias amostrais de X e Y.
Nessas condições se P(|V|< 0,32) = 0,80, o valor de n é

O peso de determinado produto é uma variável aleatória X com distribuição normal com média µ (kg) e variância σ² (kg)² . Sabe-se que 90% dos valores de X estão compreendidos entre (µ - 0,41)kg e (µ + 0,41)kg e que 85% dos valores de X são superiores a 1 kg. Nessas condições, o valor de µ, em kg, é