2. Questões de Concurso

Filtrar

Questões por página:

Seja (X, Y) uma variável bidimensional contínua com função densidade de probabilidade conjunta dada por 

Nessas condições, a esperança condicional de Y dado que X = 1/4 , é dada por

Sejam X e Y duas variáveis aleatórias independentes. Sabe-se que X tem distribuição binomial com parâmetros n = 2 e p = 0,3 e que Y tem distribuição uniforme discreta no intervalo, fechado, de números inteiros [2, 4]. Nessas condições P(X + Y ≤ 4) é igual a

A tabela abaixo apresenta a distribuição conjunta de probabilidades das variáveis XA e XB, onde XA representa os preços, em reais, do produto A e XB os preços, em reais, do produto B.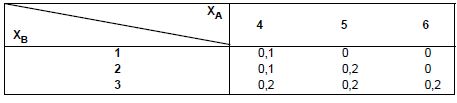



Uma peça é composta por 5 unidades do produto A e 4 unidades do produto B. Seja Z o preço dessa peça. Nessas condições, a probabilidade condicional dada por P (XA ≤ 5|XB ≥ 2) e a média de Z, são dadas, respectivamente, por

A quantia (em milhões de reais) gasta anualmente em suprimentos de papelaria em um determinado órgão governamental é uma variável aleatória X com função densidade de probabilidade dada por 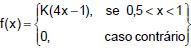 , onde K é uma constante apropriada para garantir que f(x) seja uma função densidade de probabilidade. Nessas condições o valor de K é igual a

O tempo de espera, em meses, para a concessão de certa licença ambiental em um órgão responsável por tais licenças é uma variável aleatória X com distribuição exponencial com média de 2 meses. A probabilidade condicional de X ser superior a 2 meses, sabendo-se que X foi, no máximo, igual a 3 meses é igual a

Dados:
e-1 = 0,368
e-1,5 = 0,223
e-2 = 0,135
© 2016-2025 Fonte Concursos - Questões de Concurso e Plano de Estudo