Questões de Concurso
Filtrar
3.627 Questões de concurso encontradas
Página 9 de 726
Questões por página:

Com base na tabela, o valor da mediana desta corrida é igual a:
Julgue o item a seguir.
Se a mediana e a moda de um conjunto de dados são iguais, isso implica que todos os valores do conjunto também são iguais entre si. Por exemplo, considere o conjunto de dados {5,5,5,5,5}. Neste caso, tanto a mediana quanto a moda são iguais a 5, e todos os valores no conjunto são iguais entre si.
Julgue o item a seguir.
A média aritmética ponderada de um conjunto de dados sempre será maior do que a média aritmética simples se os pesos atribuídos aos valores maiores forem superiores aos pesos dos valores menores. Por exemplo, considere os valores 2,4, e 6, com pesos 1,2, e 3, respectivamente. A média aritmética simples é 4 (calculada como (2 + 4 + 6) / 3), enquanto a média ponderada é 4.67 (calculada como (12 + 24 + 3*6) / (1 + 2 + 3)), que é maior.
Uma empresa de engenharia, que realizava o controle tecnológico de um concreto de cimento Portland, obteve, para dada amostra, que a média aritmética da resistência à compressão de corpos de prova ensaiados aos 28 dias de idade foi de 34,5 MPa, com desvio padrão de 4 MPa.
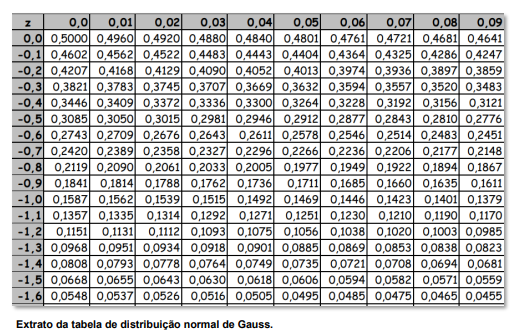
Sabendo-se que a resistência característica (fck28) corresponde ao quantil de 5 % na distribuição normal de Gauss, é correto afirmar que