Questões de Concurso
Filtrar
502.342 Questões de concurso encontradas
Página 2046 de 100.469
Questões por página:
Questões por página:
Durante uma análise estatística de séries históricas de acidentes em estradas, utilizou-se a biblioteca scipy.stats para realizar testes de hipóteses sobre a média de um conjunto de dados amostrais normalmente distribuídos com variância desconhecida. O código utilizado foi:
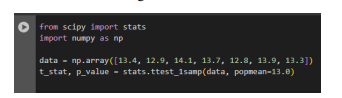
Transcrição da imagem: from spicy import stats import numpy as np data = np.array([13.4,12.9,14.1,13.7,12.8,13.9,13.3]) t_stat, p_value = stats.ttest_1samp(data, popmean=13.0)
Com base nesse código e nos fundamentos de estatística inferencial, AFIRMA-SE que:

Transcrição da imagem: from spicy import stats import numpy as np data = np.array([13.4,12.9,14.1,13.7,12.8,13.9,13.3]) t_stat, p_value = stats.ttest_1samp(data, popmean=13.0)
Com base nesse código e nos fundamentos de estatística inferencial, AFIRMA-SE que:
Um cientista atuarial está desenvolvendo um modelo para classificar apólices de seguro corporativo com base em três critérios conflitantes: risco de sinistro (a ser minimizado), rentabilidade esperada (a ser maximizada) e nível de fidelização do cliente (a ser maximizado). Para aplicar um método de ponderação aditiva compensatória, ele atribui pesos a cada critério e normaliza os dados em uma escala comum. Durante a análise, percebe que uma apólice com alto risco de sinistro obteve pontuação final superior a outra com risco baixo, mas rentabilidade e fidelização apenas medianas.
Com base nessa situação e nos princípios dos métodos de multicritério, é CORRETO afirmar que:
Com base nessa situação e nos princípios dos métodos de multicritério, é CORRETO afirmar que:
Um teste para detectar uma manifestação infecciosa, foi desenvolvido em uma universidade com uma eficiência estimada em 95%. Porém, o teste aponta um resultado falso positivo para 1% das pessoas sadias testadas. Se 0,5% da população tem a doença, a probabilidade de uma pessoa ter essa infecção, dado que o resultado de seu exame foi positivo, é:
Em um torneio de bilas, também chamadas de “bolas de gude”, quatro crianças, Adriano, Bruno, César e Daniel, vão brincar apostando cada um dez bilas. Sabe-se que Adriano é um dos que mais brincam, o que lhe garante três vezes mais chances de ganhar do Bruno. Ao mesmo tempo, é duas vezes mais provável que Bruno ganhe de César e três vezes mais provável que César ganhe de Daniel. Logo, a probabilidade de César ganhar é:
Um determinado conjunto A = {α1, α2, ⋯, αn} possui média μA e variância σ 2A . Aplica-se sobre o conjunto A as seguintes operações: bi = 3 ⋅ αi + 2, ∀i = 1,2, ⋯, n. Portanto, a média μB e a variância σ 2B do conjunto B = {b1, b2, ⋯, bn } são, respectivamente: